Code
# R's ML approach emphasizes:
# - Statistical interpretability
# - Model diagnostics
# - Uncertainty quantification
# - Research reproducibility
# - Academic rigorJune 19, 2025
While Python dominates in deep learning and engineering-focused machine learning, R provides unique advantages through its statistical foundation. R’s approach to machine learning emphasizes interpretability, statistical rigor, and research-grade implementations that complement Python’s strengths.
R’s machine learning is grounded in statistical theory:
R provides peer-reviewed machine learning packages:
R excels in statistical learning:
Call:
lm(formula = mpg ~ wt + cyl + hp, data = mtcars)
Residuals:
Min 1Q Median 3Q Max
-3.9290 -1.5598 -0.5311 1.1850 5.8986
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 38.75179 1.78686 21.687 < 2e-16 ***
wt -3.16697 0.74058 -4.276 0.000199 ***
cyl -0.94162 0.55092 -1.709 0.098480 .
hp -0.01804 0.01188 -1.519 0.140015
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2.512 on 28 degrees of freedom
Multiple R-squared: 0.8431, Adjusted R-squared: 0.8263
F-statistic: 50.17 on 3 and 28 DF, p-value: 2.184e-11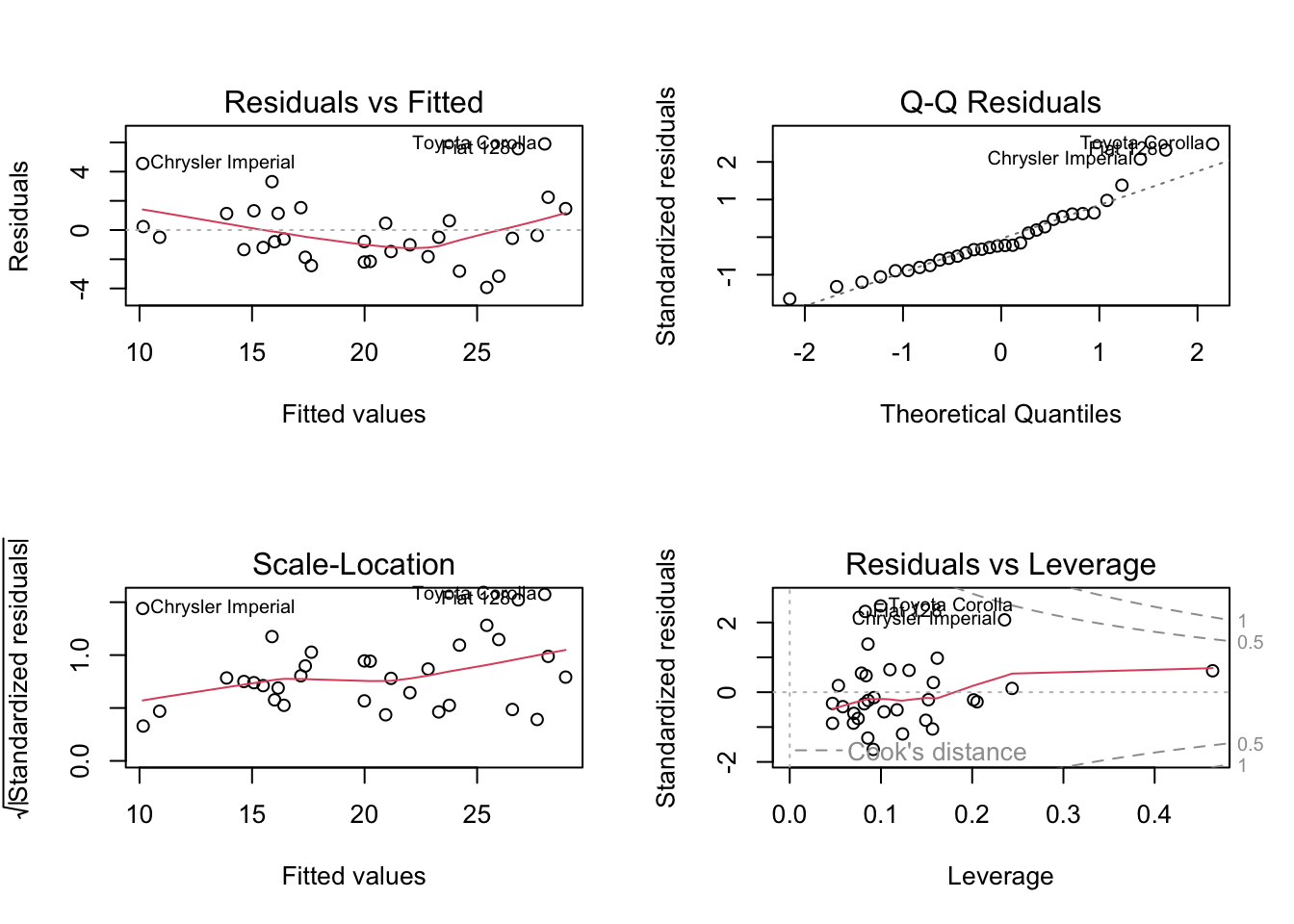
Start: AIC=62.66
mpg ~ wt + cyl + hp
Df Sum of Sq RSS AIC
<none> 176.62 62.665
- hp 1 14.551 191.17 63.198
- cyl 1 18.427 195.05 63.840
- wt 1 115.354 291.98 76.750R provides sophisticated GAM implementations:
Call: gam(formula = mpg ~ s(wt) + s(hp) + cyl, data = mtcars)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.4914 -1.3267 -0.1171 0.9720 4.4302
(Dispersion Parameter for gaussian family taken to be 4.5484)
Null Deviance: 1126.047 on 31 degrees of freedom
Residual Deviance: 100.0641 on 22 degrees of freedom
AIC: 149.2945
Number of Local Scoring Iterations: NA
Anova for Parametric Effects
Df Sum Sq Mean Sq F value Pr(>F)
s(wt) 1 777.91 777.91 171.0300 7.491e-12 ***
s(hp) 1 97.78 97.78 21.4982 0.0001274 ***
cyl 1 5.16 5.16 1.1351 0.2982414
Residuals 22 100.06 4.55
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Anova for Nonparametric Effects
Npar Df Npar F Pr(F)
(Intercept)
s(wt) 3 2.4696 0.0887 .
s(hp) 3 2.0110 0.1418
cyl
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1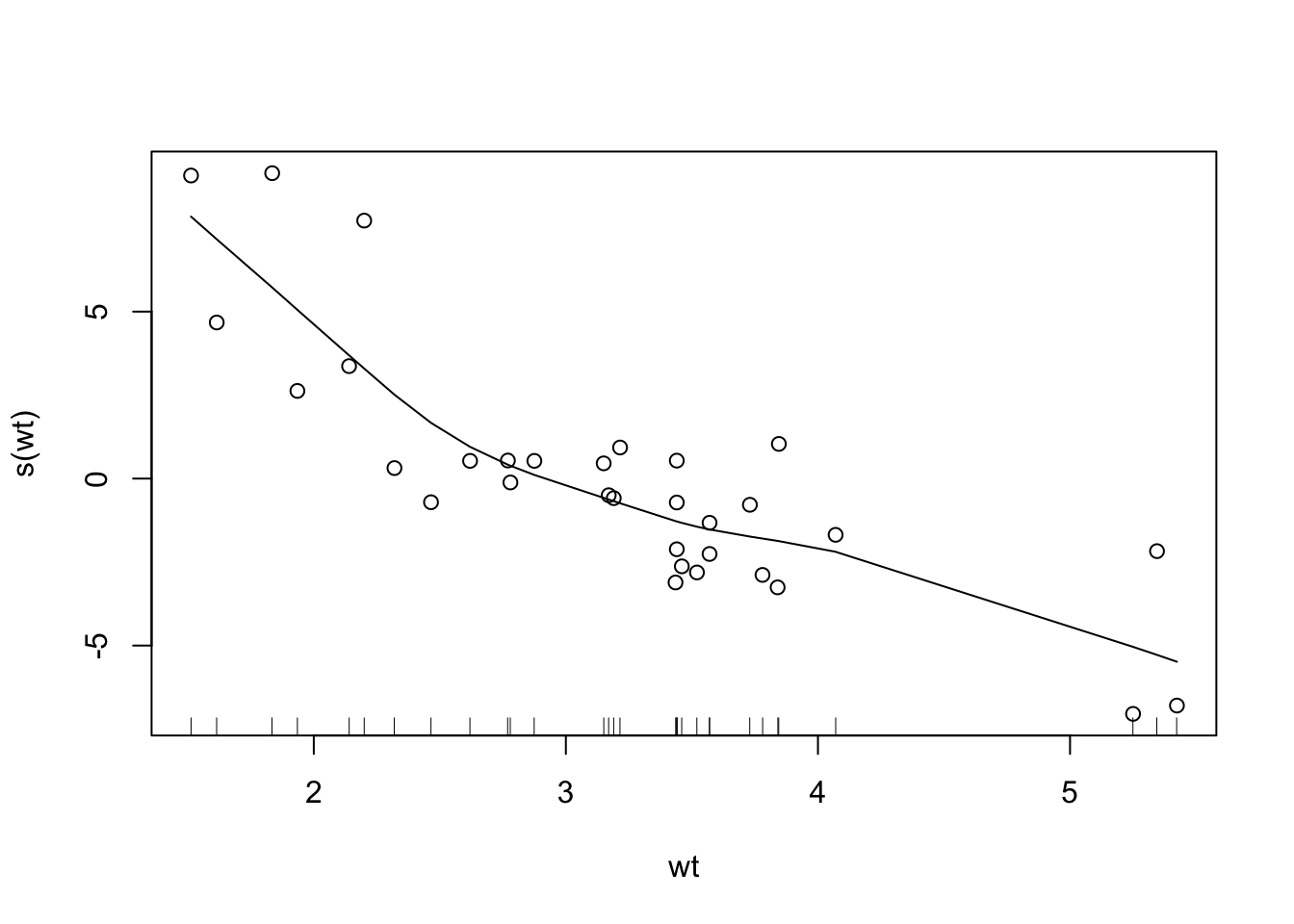

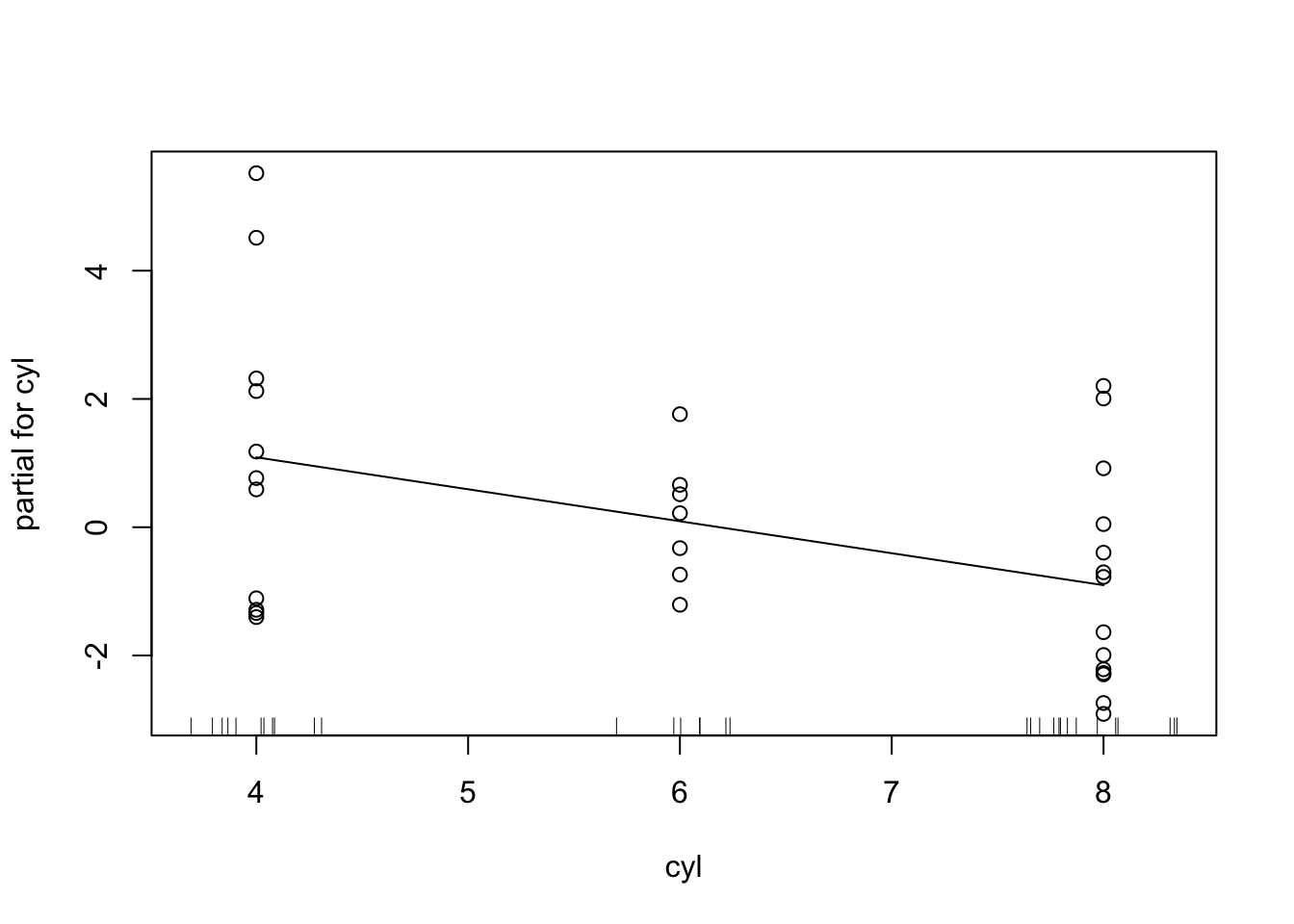
R provides statistical random forest implementations:
%IncMSE IncNodePurity
cyl 12.018647 171.22142
disp 13.841118 243.56787
hp 13.021209 171.33283
drat 5.458246 63.95108
wt 13.350573 252.46253
qsec 4.700660 33.96053
vs 3.355649 28.72671
am 3.018233 18.42451
gear 3.585899 13.51445
carb 6.095955 39.07480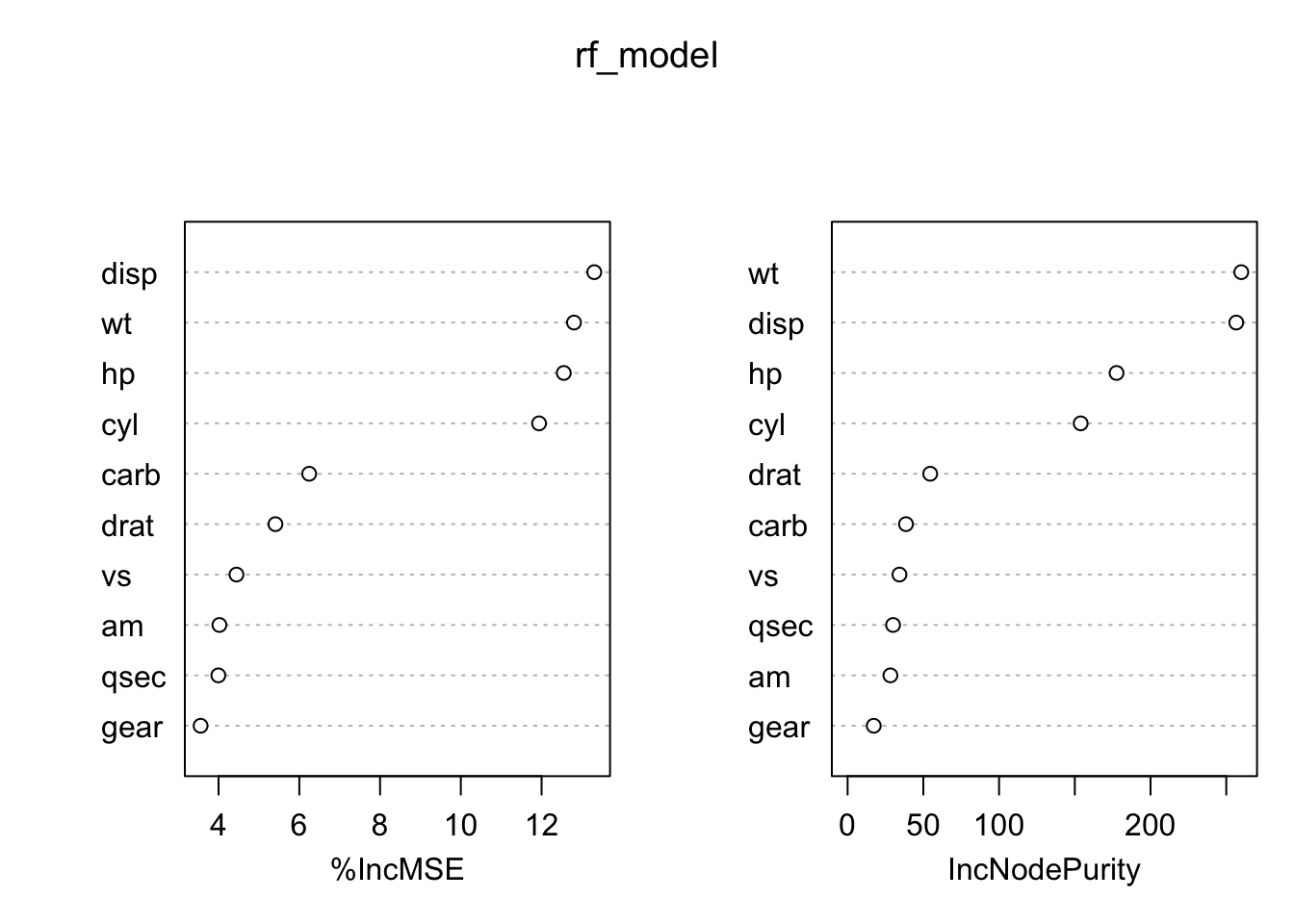
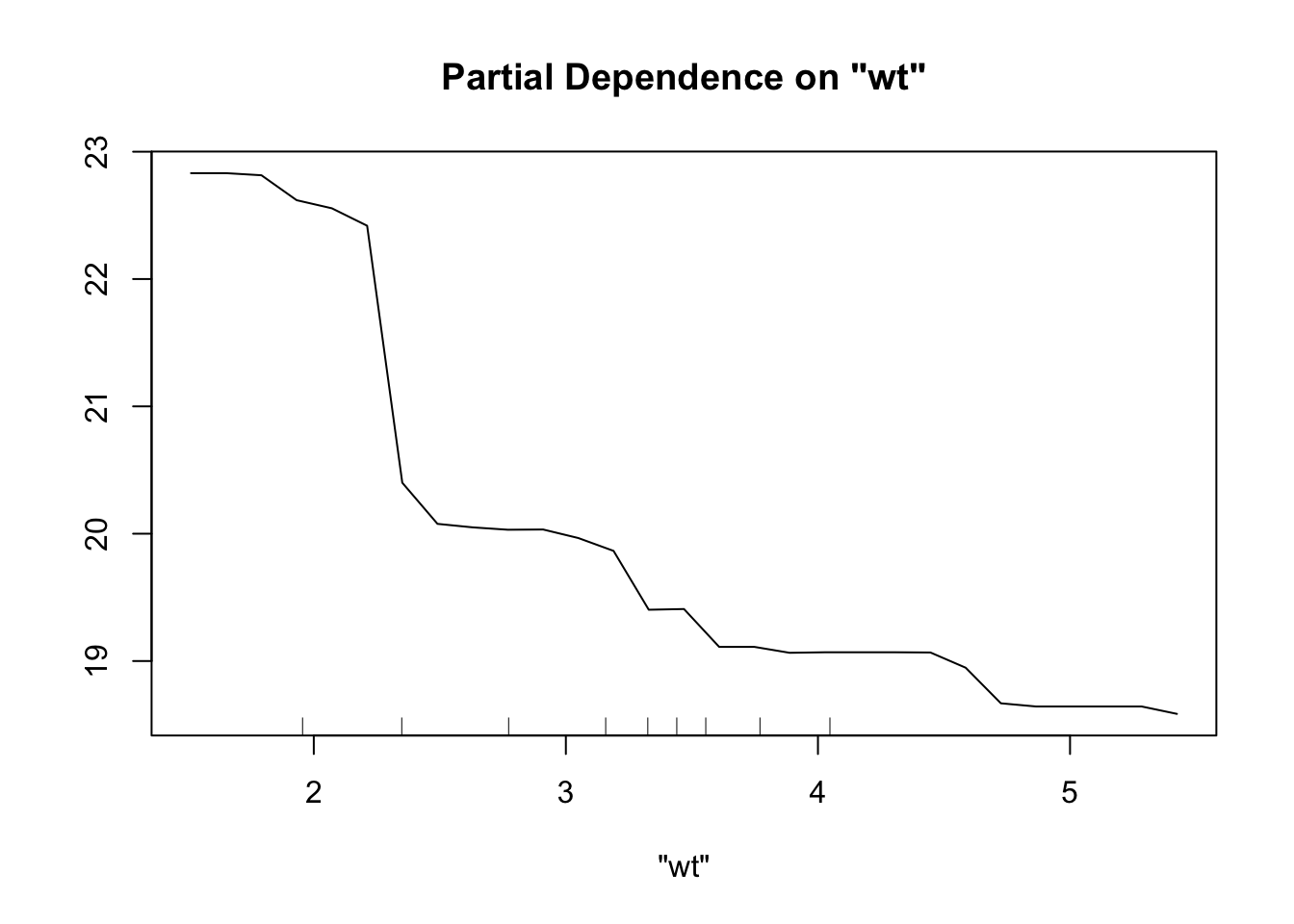
R excels in statistical gradient boosting:
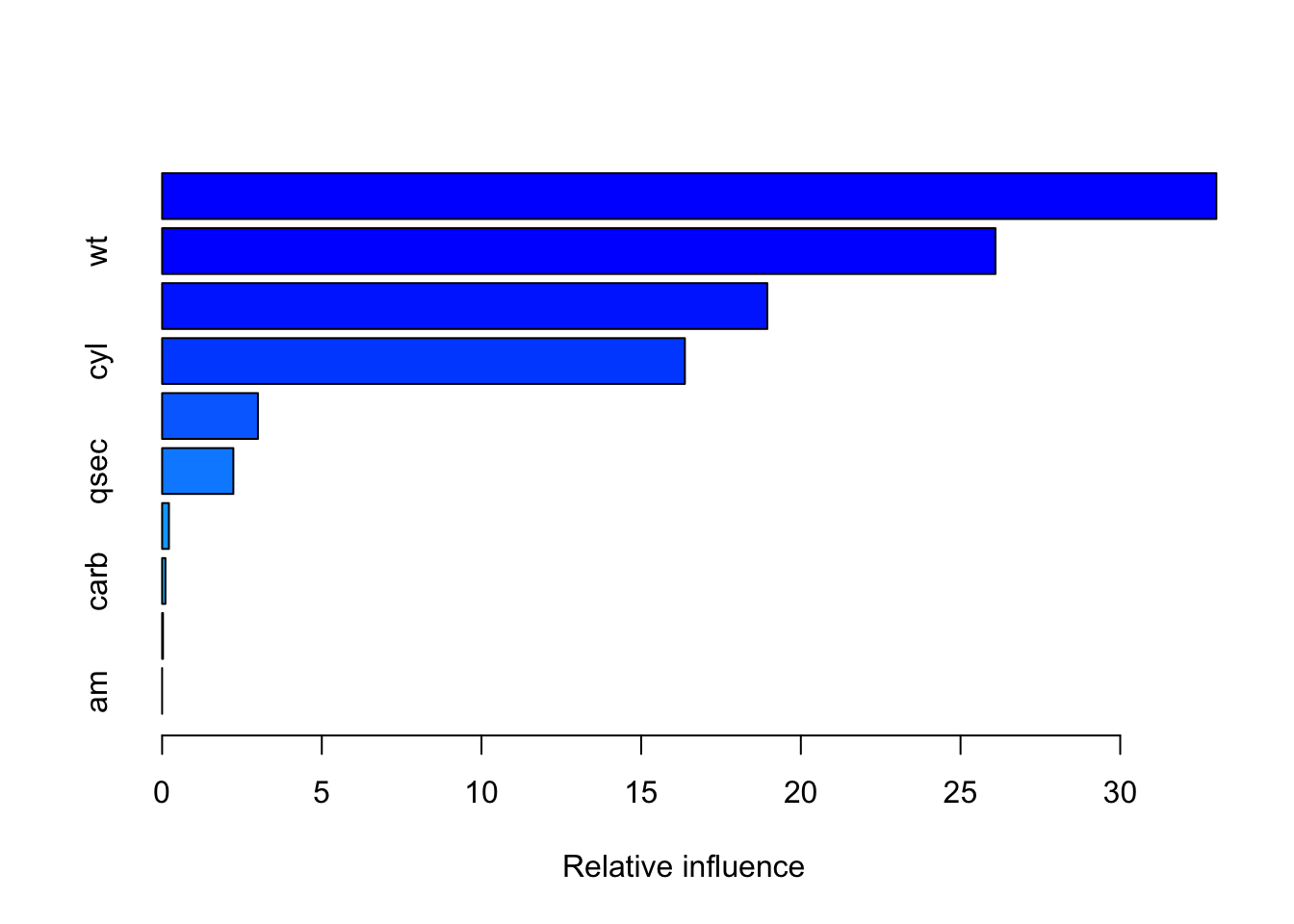
var rel.inf
disp disp 30.0403432
hp hp 23.4871419
cyl cyl 21.6488418
wt wt 18.8655558
drat drat 3.3751069
qsec qsec 2.2824743
gear gear 0.1957857
carb carb 0.1047504
vs vs 0.0000000
am am 0.0000000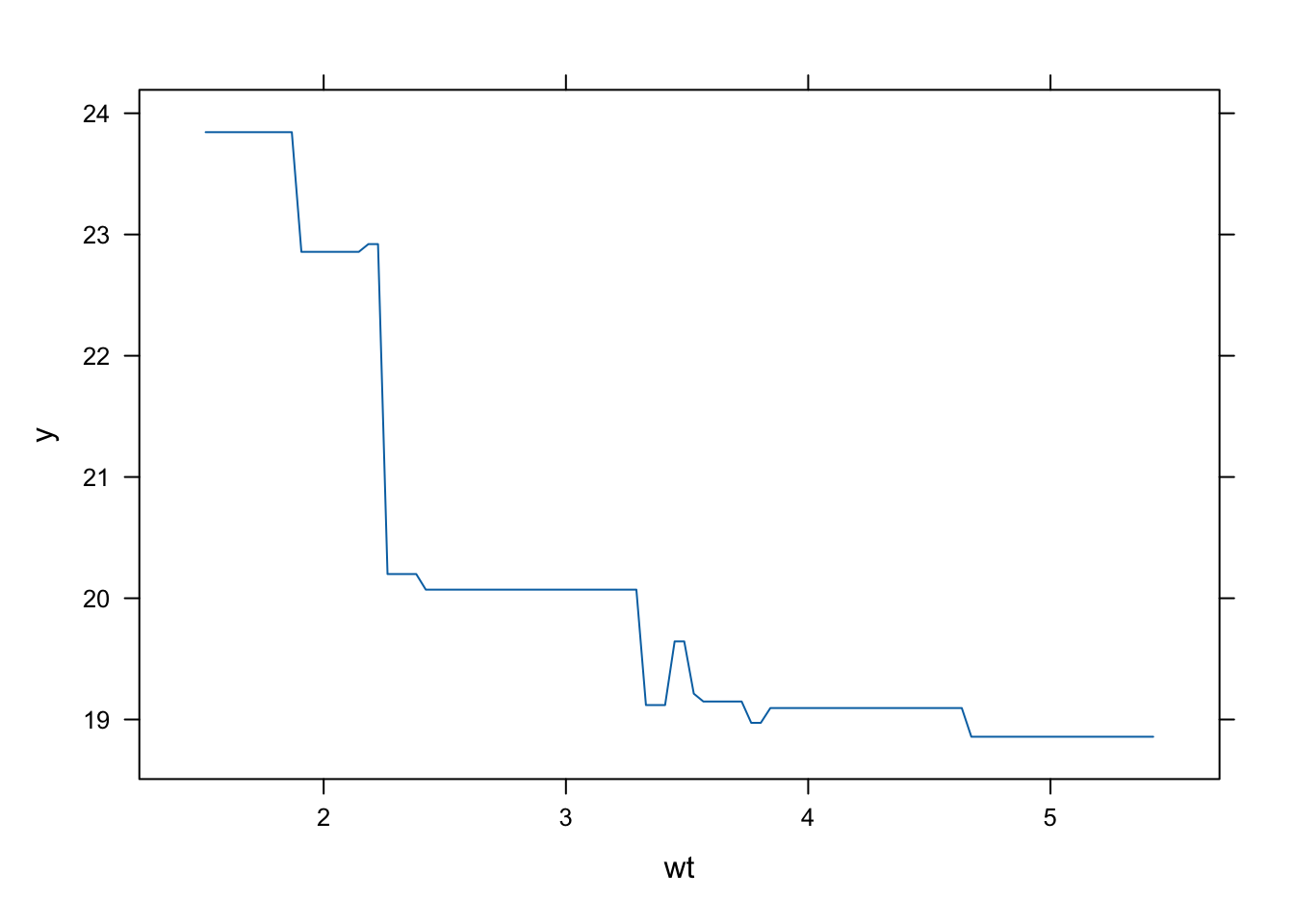
R provides comprehensive validation tools:
[1] NaN NaNR excels in model diagnostics:
Test stat Pr(>|Test stat|)
wt 2.6276 0.014007 *
cyl 1.6311 0.114476
hp 1.8147 0.080701 .
Tukey test 3.2103 0.001326 **
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1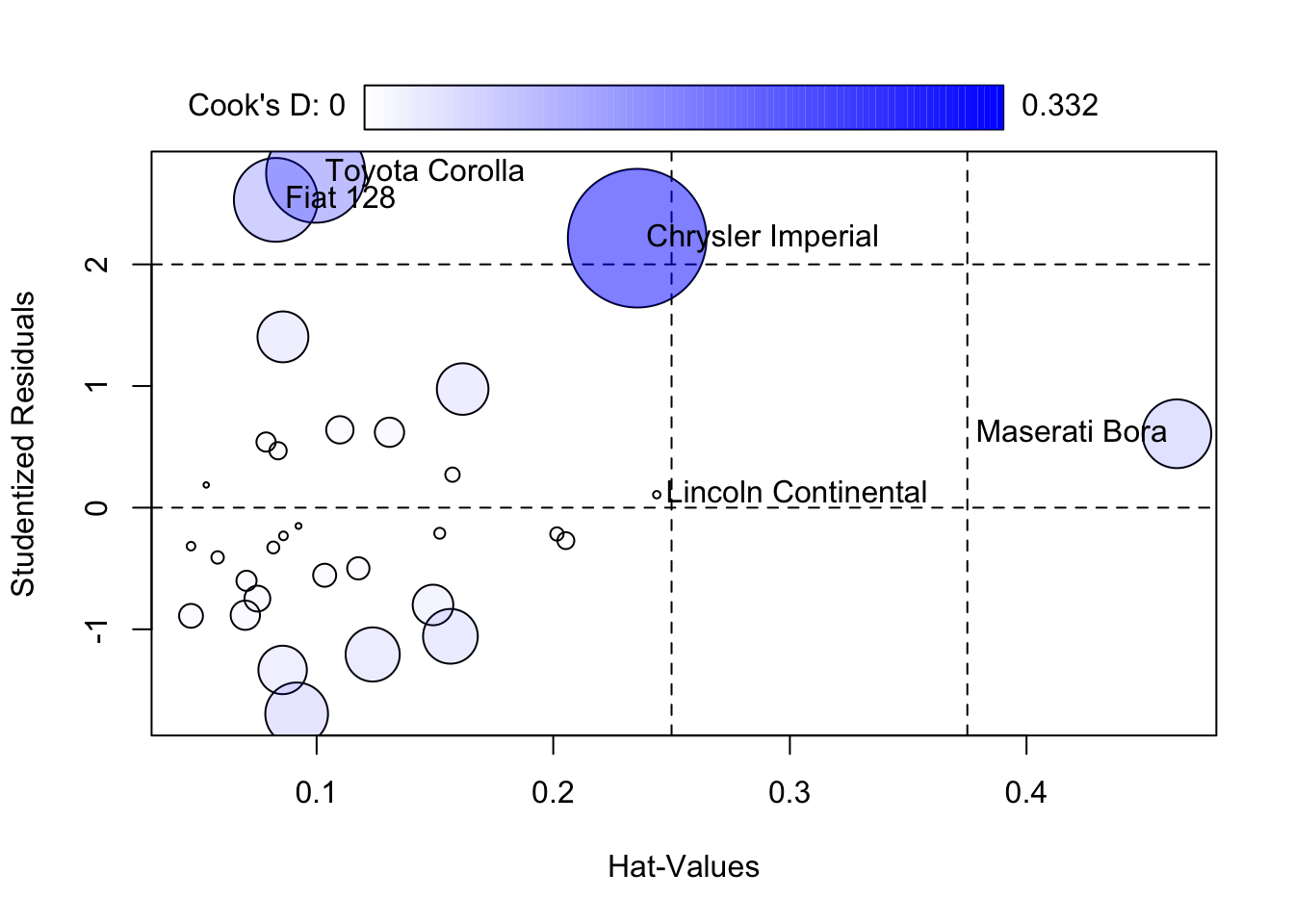
StudRes Hat CookD
Lincoln Continental 0.1065775 0.24373270 0.0009486833
Chrysler Imperial 2.2153833 0.23547715 0.3316313326
Fiat 128 2.5303244 0.08274176 0.1210330843
Toyota Corolla 2.7498370 0.09961207 0.1694339333
Maserati Bora 0.6073374 0.46356582 0.0815260489 wt cyl hp
2.580486 4.757456 3.258481
Shapiro-Wilk normality test
data: residuals(lm_model)
W = 0.93455, p-value = 0.05252R provides sophisticated Bayesian ML:
SAMPLING FOR MODEL 'continuous' NOW (CHAIN 1).
Chain 1:
Chain 1: Gradient evaluation took 0.00078 seconds
Chain 1: 1000 transitions using 10 leapfrog steps per transition would take 7.8 seconds.
Chain 1: Adjust your expectations accordingly!
Chain 1:
Chain 1:
Chain 1: Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 1: Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 1: Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 1: Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 1: Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 1: Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 1: Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 1: Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 1: Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 1: Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 1: Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 1: Iteration: 2000 / 2000 [100%] (Sampling)
Chain 1:
Chain 1: Elapsed Time: 0.024 seconds (Warm-up)
Chain 1: 0.025 seconds (Sampling)
Chain 1: 0.049 seconds (Total)
Chain 1:
SAMPLING FOR MODEL 'continuous' NOW (CHAIN 2).
Chain 2:
Chain 2: Gradient evaluation took 3e-06 seconds
Chain 2: 1000 transitions using 10 leapfrog steps per transition would take 0.03 seconds.
Chain 2: Adjust your expectations accordingly!
Chain 2:
Chain 2:
Chain 2: Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 2: Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 2: Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 2: Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 2: Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 2: Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 2: Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 2: Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 2: Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 2: Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 2: Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 2: Iteration: 2000 / 2000 [100%] (Sampling)
Chain 2:
Chain 2: Elapsed Time: 0.025 seconds (Warm-up)
Chain 2: 0.02 seconds (Sampling)
Chain 2: 0.045 seconds (Total)
Chain 2:
SAMPLING FOR MODEL 'continuous' NOW (CHAIN 3).
Chain 3:
Chain 3: Gradient evaluation took 3e-06 seconds
Chain 3: 1000 transitions using 10 leapfrog steps per transition would take 0.03 seconds.
Chain 3: Adjust your expectations accordingly!
Chain 3:
Chain 3:
Chain 3: Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 3: Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 3: Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 3: Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 3: Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 3: Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 3: Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 3: Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 3: Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 3: Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 3: Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 3: Iteration: 2000 / 2000 [100%] (Sampling)
Chain 3:
Chain 3: Elapsed Time: 0.026 seconds (Warm-up)
Chain 3: 0.024 seconds (Sampling)
Chain 3: 0.05 seconds (Total)
Chain 3:
SAMPLING FOR MODEL 'continuous' NOW (CHAIN 4).
Chain 4:
Chain 4: Gradient evaluation took 3e-06 seconds
Chain 4: 1000 transitions using 10 leapfrog steps per transition would take 0.03 seconds.
Chain 4: Adjust your expectations accordingly!
Chain 4:
Chain 4:
Chain 4: Iteration: 1 / 2000 [ 0%] (Warmup)
Chain 4: Iteration: 200 / 2000 [ 10%] (Warmup)
Chain 4: Iteration: 400 / 2000 [ 20%] (Warmup)
Chain 4: Iteration: 600 / 2000 [ 30%] (Warmup)
Chain 4: Iteration: 800 / 2000 [ 40%] (Warmup)
Chain 4: Iteration: 1000 / 2000 [ 50%] (Warmup)
Chain 4: Iteration: 1001 / 2000 [ 50%] (Sampling)
Chain 4: Iteration: 1200 / 2000 [ 60%] (Sampling)
Chain 4: Iteration: 1400 / 2000 [ 70%] (Sampling)
Chain 4: Iteration: 1600 / 2000 [ 80%] (Sampling)
Chain 4: Iteration: 1800 / 2000 [ 90%] (Sampling)
Chain 4: Iteration: 2000 / 2000 [100%] (Sampling)
Chain 4:
Chain 4: Elapsed Time: 0.023 seconds (Warm-up)
Chain 4: 0.024 seconds (Sampling)
Chain 4: 0.047 seconds (Total)
Chain 4: 5% 95%
(Intercept) 36.706368 42.6259745
wt -4.438626 -1.9209506
cyl -2.207312 -0.7992415
sigma 2.134191 3.2862048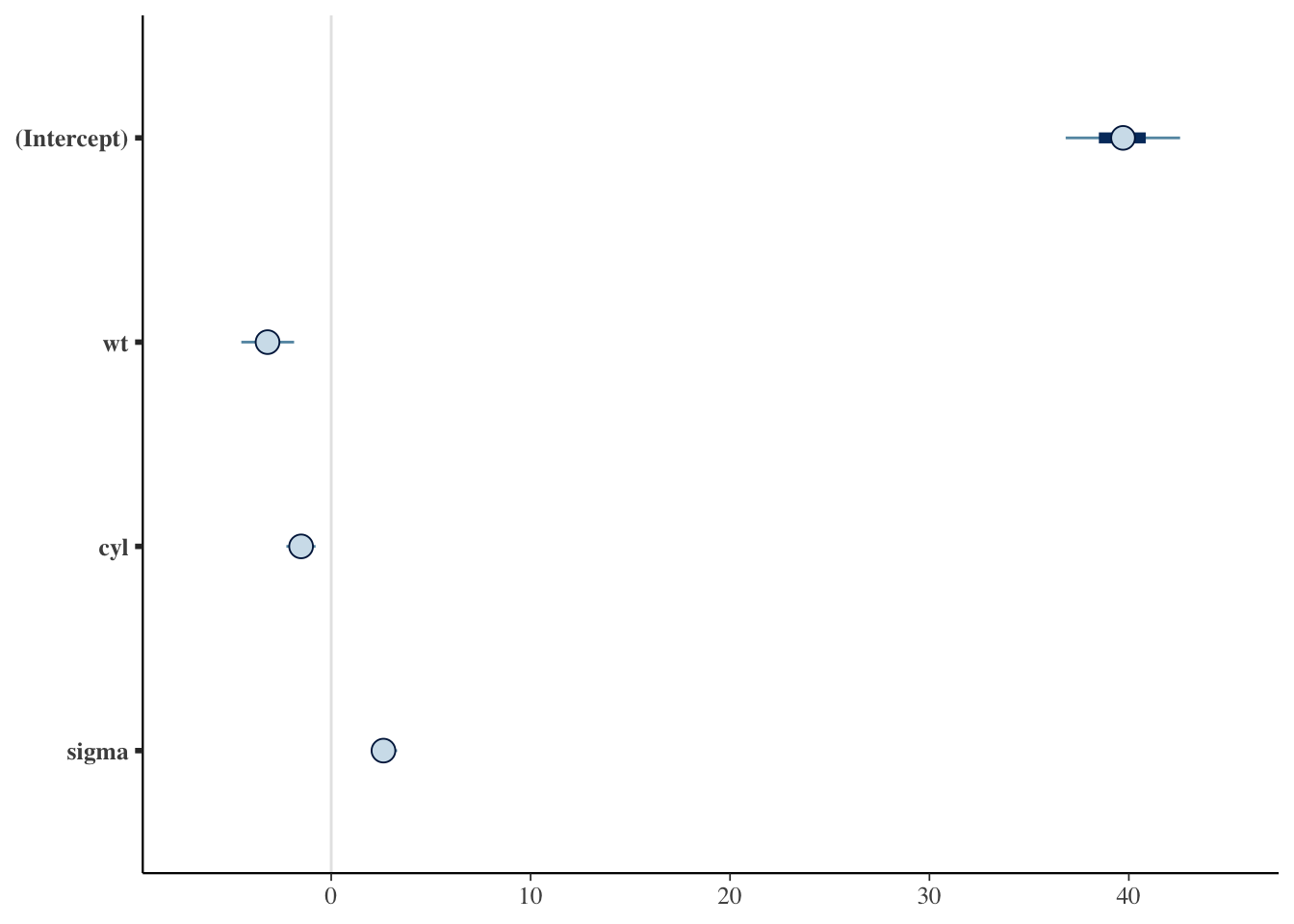
R excels in probabilistic programming:
R emphasizes model interpretability:
R provides explainable AI tools:
Python’s ML is engineering-focused:
Python lacks statistical depth:
| Feature | R | Python |
|---|---|---|
| Statistical Foundation | Excellent | Limited |
| Model Diagnostics | Comprehensive | Basic |
| Interpretability | Advanced | Limited |
| Research Integration | Strong | Weak |
| Uncertainty Quantification | Sophisticated | Basic |
| Academic Validation | Peer-reviewed | Variable |
| Deep Learning | Limited | Excellent |
| Production Deployment | Limited | Excellent |
R and Python can complement each other:
R’s machine learning approach provides:
While Python excels in deep learning and production deployment, R provides unique advantages for statistical machine learning, research, and interpretable AI applications.
This concludes our series on “R Beats Python” - exploring the specific areas where R provides superior capabilities for data science and statistical analysis.
---
title: "Machine Learning: R's Statistical Approach"
description: "How R's statistical foundation provides unique advantages for machine learning compared to Python's engineering-focused approach"
date: 2025-06-19
categories: [machine-learning, statistics, modeling]
---
## Introduction
While Python dominates in deep learning and engineering-focused machine learning, R provides unique advantages through its statistical foundation. R's approach to machine learning emphasizes interpretability, statistical rigor, and research-grade implementations that complement Python's strengths.
## R's Statistical ML Foundation
### Built on Statistical Theory
R's machine learning is grounded in statistical theory:
```{r}
#| echo: true
# R's ML approach emphasizes:
# - Statistical interpretability
# - Model diagnostics
# - Uncertainty quantification
# - Research reproducibility
# - Academic rigor
```
### Research-Grade Implementations
R provides peer-reviewed machine learning packages:
```{r}
#| echo: true
# R's ML packages are:
# - Peer-reviewed
# - Published in statistical journals
# - Used in academic research
# - Well-documented
# - Statistically validated
```
## Statistical Learning with R
### Linear and Generalized Linear Models
R excels in statistical learning:
```{r}
#| echo: true
library(stats)
library(MASS)
# Linear models with comprehensive diagnostics
lm_model <- lm(mpg ~ wt + cyl + hp, data = mtcars)
summary(lm_model)
# Model diagnostics
par(mfrow = c(2, 2))
plot(lm_model)
# Stepwise selection
step_model <- stepAIC(lm_model, direction = "both")
```
### Generalized Additive Models
R provides sophisticated GAM implementations:
```{r}
#| echo: true
library(mgcv)
library(gam)
# Generalized additive models
gam_model <- gam(mpg ~ s(wt) + s(hp) + cyl, data = mtcars)
# Model summary with significance tests
summary(gam_model)
# Visualization of smooth terms
plot(gam_model, residuals = TRUE)
```
## Ensemble Methods
### Random Forests
R provides statistical random forest implementations:
```{r}
#| echo: true
library(randomForest)
# Random forest with statistical output
rf_model <- randomForest(mpg ~ ., data = mtcars, importance = TRUE)
# Variable importance with statistical significance
importance(rf_model)
varImpPlot(rf_model)
# Partial dependence plots
partialPlot(rf_model, mtcars, "wt")
```
### Gradient Boosting
R excels in statistical gradient boosting:
```{r}
#| echo: true
library(gbm)
# Gradient boosting with statistical diagnostics
# Adjusted parameters for small dataset
gbm_model <- gbm(mpg ~ ., data = mtcars,
distribution = "gaussian",
n.trees = 100,
interaction.depth = 2,
bag.fraction = 0.8,
n.minobsinnode = 3)
# Variable importance
summary(gbm_model)
# Partial dependence plots
plot(gbm_model, i.var = "wt")
```
## Model Diagnostics and Validation
### Cross-Validation
R provides comprehensive validation tools:
```{r}
#| echo: true
library(caret)
library(boot)
# Cross-validation with statistical rigor
cv_results <- cv.glm(mtcars, lm_model, K = 10)
cv_results$delta
# Caret for systematic model comparison
control <- trainControl(method = "cv", number = 10)
model_comparison <- train(mpg ~ ., data = mtcars,
method = "rf",
trControl = control)
```
### Model Diagnostics
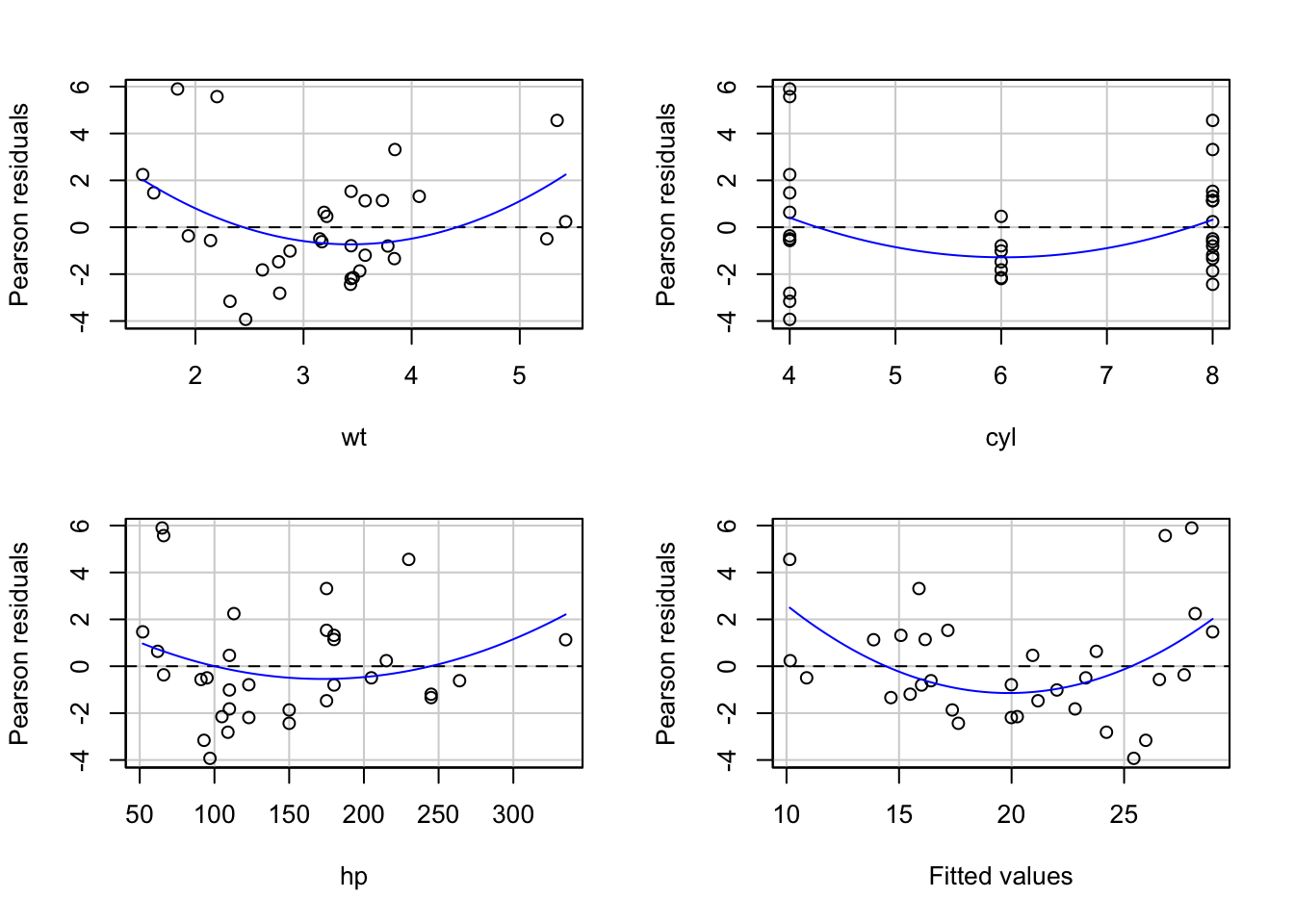
R excels in model diagnostics:
```{r}
#| echo: true
# Comprehensive model diagnostics
library(car)
# Residual analysis
residualPlots(lm_model)
# Influence diagnostics
influencePlot(lm_model)
# Multicollinearity
vif(lm_model)
# Normality tests
shapiro.test(residuals(lm_model))
```
## Bayesian Machine Learning
### Bayesian Models
R provides sophisticated Bayesian ML:
```{r}
#| echo: true
library(rstan)
library(brms)
library(rstanarm)
# Bayesian linear regression
bayes_model <- stan_glm(mpg ~ wt + cyl, data = mtcars,
family = gaussian(),
prior = normal(0, 10))
# Posterior analysis
posterior_interval(bayes_model)
plot(bayes_model)
```
### Probabilistic Programming
R excels in probabilistic programming:
```{r}
#| echo: true
# Stan integration for complex models
# - Hierarchical models
# - Time series models
# - Spatial models
# - Custom likelihoods
# - Advanced inference
```
## Interpretable Machine Learning
### Model Interpretability
R emphasizes model interpretability:
```{r}
#| echo: true
library(iml)
library(DALEX)
# Model interpretability tools
# - Partial dependence plots
# - Individual conditional expectation
# - Feature importance
# - Model explanations
# - Fairness analysis
```
### Explainable AI
R provides explainable AI tools:
```{r}
#| echo: true
# Explainable AI capabilities
# - LIME implementation
# - SHAP values
# - Model-agnostic explanations
# - Feature interactions
# - Decision paths
```
## Python's ML Limitations
### Engineering Focus
Python's ML is engineering-focused:
```python
# Python ML emphasizes:
# - Scalability
# - Production deployment
# - Deep learning
# - Engineering efficiency
# - Less statistical rigor
```
### Limited Statistical Depth
Python lacks statistical depth:
```python
# Python has limited:
# - Statistical diagnostics
# - Model interpretability
# - Uncertainty quantification
# - Research reproducibility
# - Academic validation
```
## Performance Comparison
| Feature | R | Python |
|---------|---|--------|
| Statistical Foundation | Excellent | Limited |
| Model Diagnostics | Comprehensive | Basic |
| Interpretability | Advanced | Limited |
| Research Integration | Strong | Weak |
| Uncertainty Quantification | Sophisticated | Basic |
| Academic Validation | Peer-reviewed | Variable |
| Deep Learning | Limited | Excellent |
| Production Deployment | Limited | Excellent |
## Key Advantages of R for ML
### 1. **Statistical Rigor**
```{r}
#| echo: true
# R ensures statistical rigor in ML:
# - Proper model diagnostics
# - Uncertainty quantification
# - Statistical significance testing
# - Model validation
# - Research reproducibility
```
### 2. **Interpretability Focus**
```{r}
#| echo: true
# R emphasizes interpretability:
# - Model explanations
# - Feature importance
# - Partial dependence plots
# - Statistical inference
# - Research transparency
```
### 3. **Research Integration**
```{r}
#| echo: true
# R's ML packages are:
# - Peer-reviewed
# - Published in journals
# - Used in research
# - Well-documented
# - Statistically validated
```
## Complementary Approaches
### R + Python Integration
R and Python can complement each other:
```{r}
#| echo: true
# R for:
# - Statistical modeling
# - Model diagnostics
# - Research validation
# - Interpretability
# - Academic publishing
# Python for:
# - Deep learning
# - Production deployment
# - Large-scale processing
# - Engineering workflows
# - Web applications
```
### Best of Both Worlds
```{r}
#| echo: true
# Optimal workflow:
# 1. R for exploratory analysis and statistical modeling
# 2. Python for deep learning and production deployment
# 3. R for model interpretation and validation
# 4. Python for scaling and deployment
```
## Conclusion
R's machine learning approach provides:
- **Statistical rigor** and model diagnostics
- **Research-grade implementations** with peer review
- **Emphasis on interpretability** and transparency
- **Comprehensive validation** and uncertainty quantification
- **Academic integration** and reproducibility
- **Complementary strengths** to Python's engineering focus
While Python excels in deep learning and production deployment, R provides unique advantages for statistical machine learning, research, and interpretable AI applications.
---
*This concludes our series on "R Beats Python" - exploring the specific areas where R provides superior capabilities for data science and statistical analysis.*